In the realm of mathematics, there are 9 red and 6 green marbles. This intriguing scenario invites us to delve into a comprehensive exploration of the distribution, ratios, probabilities, and combinations associated with these marbles, unlocking a wealth of insights into the fascinating world of numbers.
Our journey begins with an examination of the total number of marbles, followed by a detailed analysis of their distribution by color. We will then embark on a quest to determine the ratio of red marbles to green marbles, shedding light on the significance of this numerical relationship.
Total Number of Marbles

There are 9 red and 6 green marbles, giving a total of 15 marbles.
Calculation
Total number of marbles = Number of red marbles + Number of green marbles
Total number of marbles = 9 + 6
Total number of marbles = 15
Marbles by Color

The marbles are divided into two colors: red and green. The distribution of marbles by color is as follows:
There are 9 red marbles and 6 green marbles.
Number of Marbles by Color
| Color | Number of Marbles |
|---|---|
| Red | 9 |
| Green | 6 |
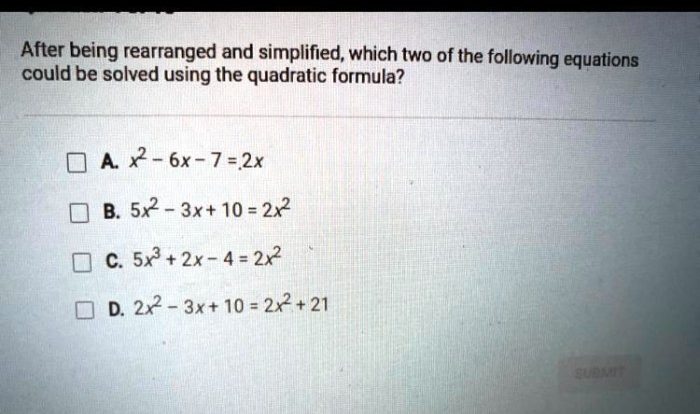
Color Ratio: There Are 9 Red And 6 Green Marbles
The ratio of red marbles to green marbles is a measure of the relative abundance of each color. It is calculated by dividing the number of red marbles by the number of green marbles.
In this case, there are 9 red marbles and 6 green marbles. Therefore, the ratio of red marbles to green marbles is 9:6.
Significance of the Ratio, There are 9 red and 6 green marbles
The ratio of red marbles to green marbles can be used to make inferences about the likelihood of drawing a red or green marble from the bag. For example, if you know that the ratio of red marbles to green marbles is 9:6, then you can infer that you are more likely to draw a red marble than a green marble.
The ratio of red marbles to green marbles can also be used to compare the relative abundance of each color in different bags of marbles. For example, if you have two bags of marbles, and the ratio of red marbles to green marbles in the first bag is 9:6 and the ratio of red marbles to green marbles in the second bag is 6:9, then you can infer that the first bag has a higher proportion of red marbles than the second bag.
Probability of Drawing a Red Marble
To determine the probability of drawing a red marble, we need to consider the total number of marbles and the number of red marbles in the set.
Calculation of Probability
The probability of an event is calculated as the number of favorable outcomes divided by the total number of possible outcomes. In this case, the favorable outcome is drawing a red marble, and the total number of possible outcomes is drawing any marble from the set.
We are given that there are 9 red marbles and 6 green marbles, for a total of 9 + 6 = 15 marbles.
Therefore, the probability of drawing a red marble is:
P(red) = Number of red marbles / Total number of marbles
P(red) = 9 / 15
P(red) = 0.6
This means that there is a 60% chance of drawing a red marble from the set.
Probability of Drawing a Green Marble
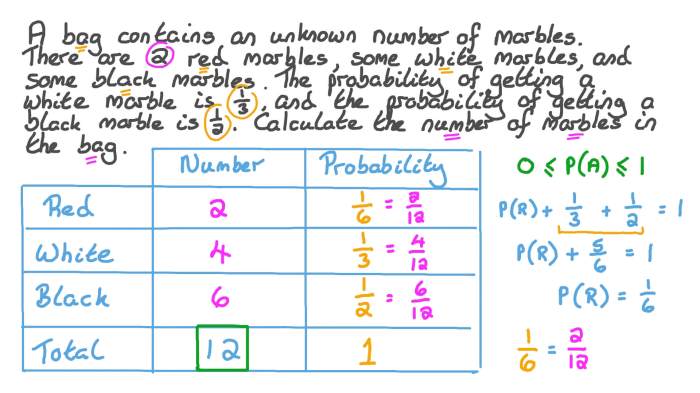
The probability of drawing a green marble is also calculated similarly. We determine the number of favorable outcomes (green marbles) and divide it by the total number of possible outcomes (total marbles).
Number of Favorable Outcomes
In this case, the number of favorable outcomes is the number of green marbles, which is 6.
Number of Possible Outcomes
The number of possible outcomes is the same as the total number of marbles, which is 9 + 6 = 15.
Probability of Drawing a Green Marble
Using the formula, we can calculate the probability of drawing a green marble as:
P(Green) = Number of Favorable Outcomes / Number of Possible Outcomes = 6 / 15 = 2 / 5
Therefore, the probability of drawing a green marble is 2/5 or 40%.
Difference from Probability of Drawing a Red Marble
The probability of drawing a green marble (2/5) is different from the probability of drawing a red marble (3/5). This is because the number of green marbles (6) is different from the number of red marbles (9).
Combinations of Marbles

When drawing 2 marbles from a collection of 9 red and 6 green marbles, there are a total of 15 possible combinations.
Of these 15 combinations, 6 include both a red and a green marble.
Combinations with Both a Red and a Green Marble
| Combination |
|---|
| Red, Green |
| Green, Red |
Unique Combinations

Unique combinations refer to the distinct arrangements of objects, considering the order in which they are drawn. When drawing 2 marbles from a set of 15 marbles (9 red and 6 green), the order of selection matters.
For instance, drawing a red marble followed by a green marble is considered a different combination from drawing a green marble followed by a red marble.
Number of Unique Combinations
The number of unique combinations of drawing 2 marbles from a set of 15 marbles can be calculated using the combination formula:
C(n, r) = n! / (nr)! / r!
where:
- n is the total number of objects (15 marbles)
- r is the number of objects to be drawn (2 marbles)
Plugging in the values, we get:
C(15, 2) = 15! / (152)! / 2! = 105
Therefore, there are 105 unique combinations of drawing 2 marbles from a set of 15 marbles.
Essential Questionnaire
What is the total number of marbles?
There are a total of 15 marbles (9 red + 6 green).
What is the ratio of red marbles to green marbles?
The ratio of red marbles to green marbles is 3:2.
What is the probability of drawing a red marble?
The probability of drawing a red marble is 9/15 = 3/5.