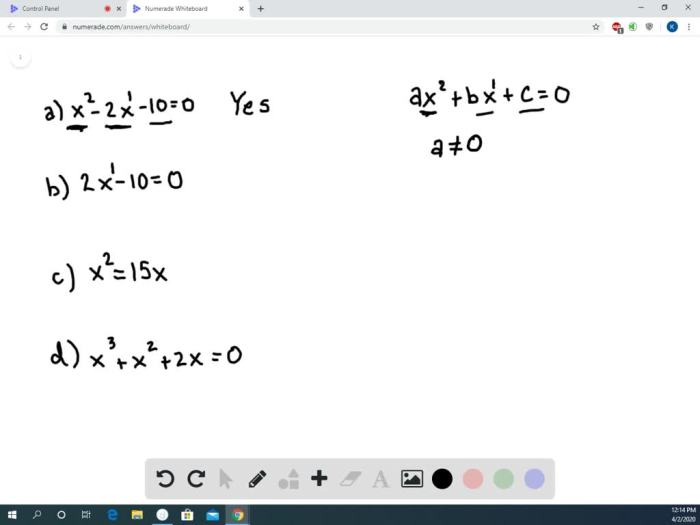
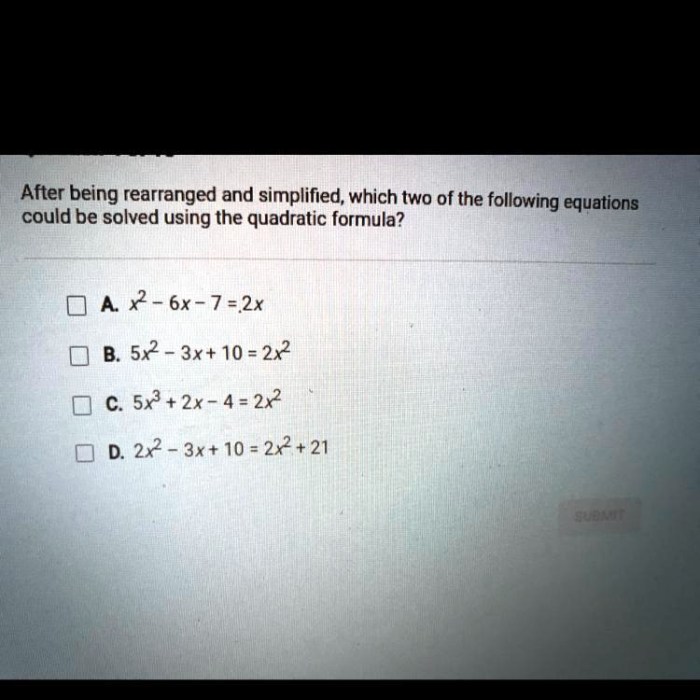
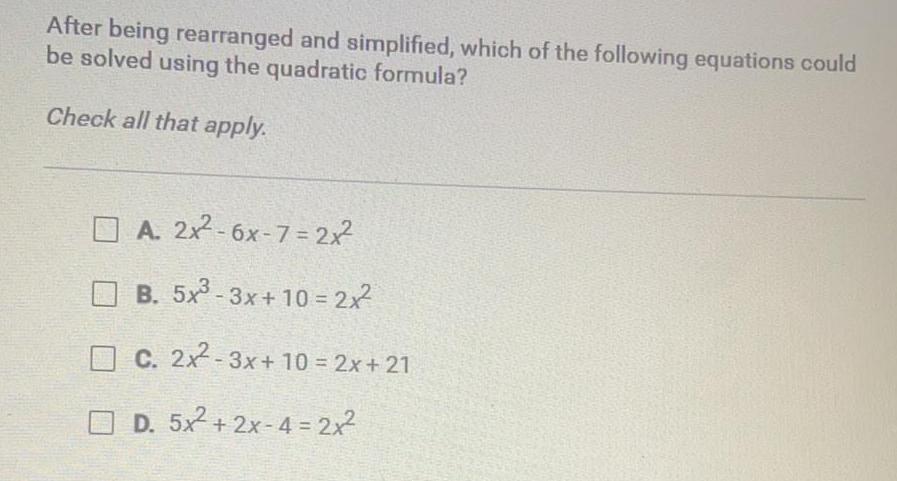After being rearranged and simplified which of the following equations – After being rearranged and simplified, which of the following equations is equivalent to the original equation? This question delves into the realm of equation manipulation, where the steps of rearrangement and simplification unveil the hidden relationships between mathematical expressions. By understanding these techniques, we gain a deeper appreciation for the power of algebra and its applications in problem-solving.

Rearranging an equation involves isolating a specific variable on one side of the equation while maintaining the equality of the expression. Simplification, on the other hand, aims to reduce the equation to its most concise form by eliminating unnecessary terms and combining like terms.

Equation Rearrangement and Simplification: After Being Rearranged And Simplified Which Of The Following Equations

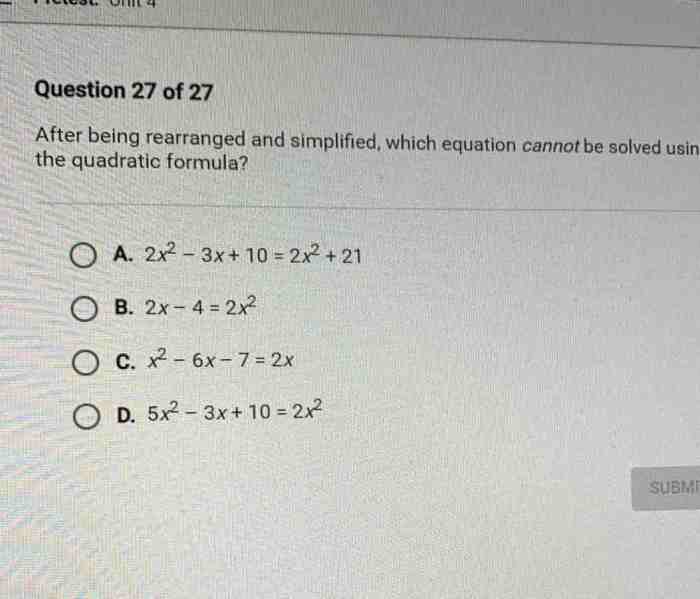
Equation rearrangement and simplification are fundamental mathematical techniques that involve manipulating equations to solve for specific variables or simplify their expressions. These techniques are widely used in various fields, including science, engineering, and economics.

Equation Rearrangement

Equation rearrangement involves transforming an equation into an equivalent form by applying mathematical operations such as addition, subtraction, multiplication, and division. The goal is to isolate the variable of interest on one side of the equation.

• Example:Rearrange the equation 2x + 5 = 11 to solve for x.
• Steps:
  1. Subtract 5 from both sides: 2x = 6
  2. Divide both sides by 2: x = 3

Equation Simplification

Equation simplification involves reducing an equation to its simplest form without changing its solution. Techniques used include combining like terms, factoring, and applying mathematical identities.

• Example:Simplify the equation (2x + 3) – (x – 5) = 0.
• Steps:
  1. Distribute the negative sign: 2x + 3- x + 5 = 0
  2. Combine like terms: x + 8 = 0
  3. Subtract 8 from both sides: x = -8

Identifying Equivalent Equations

Equivalent equations are equations that have the same solution set. Rearranging or simplifying an equation does not change its solution, resulting in equivalent equations.

These equations are equivalent because they all have the same solution set: 3, -8.

Applications of Equation Rearrangement and Simplification, After being rearranged and simplified which of the following equations

Equation rearrangement and simplification are essential techniques in various fields:

• Science:Solving equations in physics, chemistry, and biology to determine unknown variables.
• Engineering:Designing and analyzing structures, circuits, and systems.
• Economics:Modeling economic systems and forecasting trends.
• Problem-solving:Simplifying complex equations to make them easier to solve.

Query Resolution

What is the purpose of rearranging an equation?

Rearranging an equation allows us to isolate a specific variable on one side of the equation, making it easier to solve for that variable.

How does simplification differ from rearrangement?

Simplification involves reducing an equation to its most concise form by eliminating unnecessary terms and combining like terms, while rearrangement focuses on isolating a specific variable.

Why is it important to understand equivalent equations?

Equivalent equations represent the same mathematical relationship, allowing us to solve problems from different perspectives and ensuring the accuracy of our solutions.