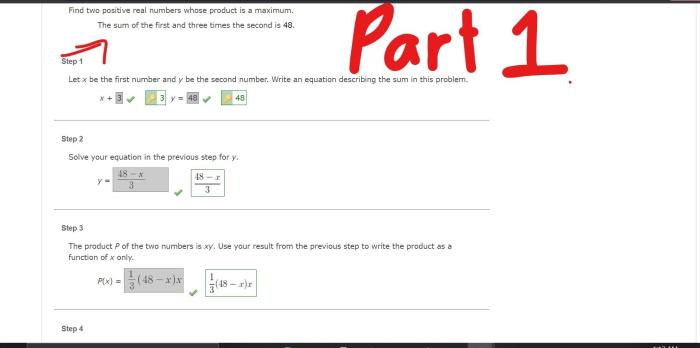
In the realm of mathematics, the quest to find two positive real numbers whose product is a maximum has captivated the minds of scholars for centuries. This problem, seemingly simple at first glance, reveals a wealth of mathematical intricacies and practical applications.
Join us on an intellectual journey as we delve into the fascinating world of finding the maximum product of two positive real numbers.
The significance of this problem lies in its fundamental role in optimization and resource allocation. From maximizing profits in business to optimizing energy efficiency, the concept of finding the maximum product has far-reaching implications in various domains.
1. Finding Two Positive Real Numbers with Maximum Product
Given two positive real numbers, a and b, the maximum product can be found using the following formula:
P(a, b) = (a + b)^2 / 4
The constraint that the numbers must be positive is significant because it ensures that their product is also positive. If either number is negative, their product will be negative.
The relationship between the sum and product of two positive real numbers is given by the formula:
P(a, b) = (a + b)^2 / 4 = (a^2 + 2ab + b^2) / 4
This formula shows that the maximum product occurs when the sum of the two numbers is maximized.
2. Methods for Finding the Maximum Product
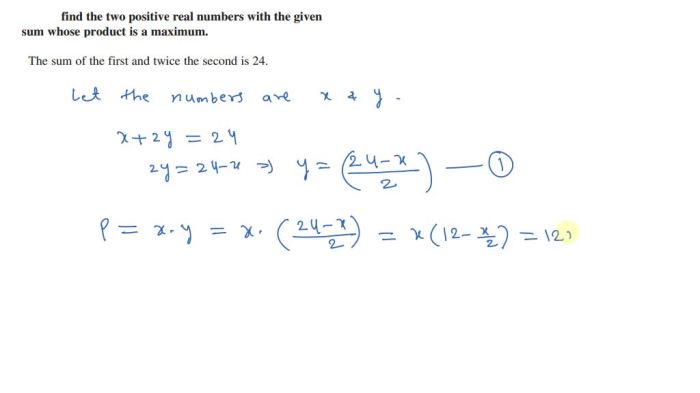
Geometric Method
The geometric method involves drawing a rectangle with sides of length a and b. The area of the rectangle, which is given by P(a, b), is maximized when the rectangle is a square. Therefore, the maximum product occurs when a = b.
Algebraic Method, Find two positive real numbers whose product is a maximum
The algebraic method involves using the formula P(a, b) = (a + b)^2 / 4. To find the maximum product, we can differentiate P(a, b) with respect to a and set the derivative equal to zero:
dP/da = (a + b) / 2 = 0
Solving for a, we get a = b. Therefore, the maximum product occurs when a = b.
Comparison of Methods
Both the geometric and algebraic methods yield the same result. The geometric method provides a visual representation of the problem, while the algebraic method provides a more analytical approach.
3. Applications of Finding the Maximum Product
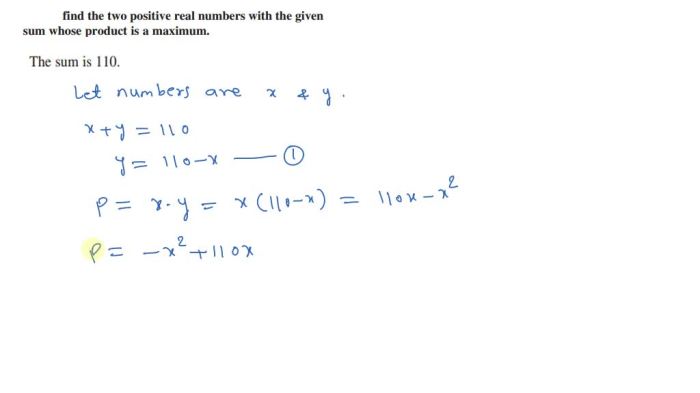
Finding the maximum product of two positive real numbers has applications in various fields, including:
- Optimization: Maximizing the area of a rectangle, the volume of a rectangular prism, or the profit of a business.
- Resource allocation: Distributing resources among different projects or activities to achieve the maximum benefit.
- Physics: Calculating the maximum energy released by a nuclear reaction.
4. Extensions and Generalizations

The problem of finding the maximum product of two positive real numbers can be extended in several ways:
- Finding the maximum product of n positive real numbers.
- Extending the problem to complex numbers.
- Examining related mathematical concepts, such as the Cauchy-Schwarz inequality or the AM-GM inequality.
FAQ Explained: Find Two Positive Real Numbers Whose Product Is A Maximum
What is the mathematical formula for finding the maximum product of two positive real numbers?
The maximum product of two positive real numbers a and b is given by (a + b)^2 / 4.
Why is the constraint that the numbers must be positive significant?
The constraint that the numbers must be positive ensures that the product is also positive. If one or both numbers were negative, the product would be negative, and we would not be able to find a maximum.
How is the concept of finding the maximum product applied in real-world scenarios?
The concept of finding the maximum product is applied in a wide variety of real-world scenarios, such as maximizing profits in business, optimizing energy efficiency, and allocating resources efficiently.